C语言算法与数据结构栈-白红宇

C语言算法与数据结构栈

阅读量：6969 次

发布时间：2019-06-27

本文共 2870 字，大约阅读时间需要 9 分钟。

栈线性数据结构的一种可以理解为操作受限的线性表

栈的特点先入后出 （可以想象一下装羽毛球的球筒，先放进去的在最底下）

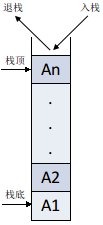
栈的表尾端称为栈顶，表头称为栈底，插入和删除都只能在栈顶操作，插入操作称为入栈，弹出操作称为出栈。

下面是栈的顺序存储结构的C实现代码

#include 
    
     #include 
     
      #define TRUE 1#define FALSE 0#define OK 1#define ERROR 0#define OVERFLOW -2#define INIT_SIZE 20#define INCREMENT_SIZE 5typedef int SElemType;typedef int Status;/* * 存储结构 */typedef struct{    SElemType *base;    //栈尾指针    SElemType *top;        //栈顶指针    int size;            //栈的大小}SqStack;/* * 初始化栈 */  Status InitStack(SqStack *S){    S->base = (SElemType*) malloc(INIT_SIZE * sizeof(SElemType));    if (!S->base)    {        exit(OVERFLOW);    }    S->top = S->base;    S->size = INIT_SIZE;    return OK;}/* * 销毁栈 */Status DestroyStack(SqStack *S){    free(S->base);    S->base = NULL;    S->top = NULL;    S->size = 0;    return OK;}/* * 清空栈 */Status ClearStack(SqStack *S){    S->top = S->base;    return OK;}/* * 判断栈是否为空 */Status IsEmpty(SqStack S){     if (S.top == S.base)    {                return TRUE;    }        else        return FALSE;}/* * 获取栈的长度 */int GetLength(SqStack S){        return (S.top - S.base) / sizeof(SElemType);}/* * 获取栈顶元素 */Status GetTop(SqStack S, SElemType *e){        if (S.top > S.base)    {        *e = *(S.top - sizeof(SElemType));                return OK;    }        else    {                return ERROR;    }}/* * 压栈 */Status Push(SqStack *S, SElemType e){        if ((S->top - S->base) / sizeof(SElemType) >= S->size)    {        S->base = (SElemType*) realloc(S->base, (S->size + INCREMENT_SIZE) * sizeof(SElemType));        if (!S->base)        {            exit(OVERFLOW);        }        S->top = S->base + S->size * sizeof(SElemType);        S->size += INCREMENT_SIZE;    }    *S->top = e;    S->top += sizeof(SElemType);        return OK;}/* * 退栈 */Status Pop(SqStack *S, SElemType *e){        if (S->top == S->base)    {                return ERROR;    }    S->top -= sizeof(SElemType);    *e = *S->top;        return OK;}/* * 访问元素 */void visit(SElemType e){    printf("%d ", e);}/* * 遍历栈 */Status TraverseStack(SqStack S, void (*visit)(SElemType)){        while (S.top > S.base)    {        visit(*S.base);        S.base += sizeof(SElemType);    }        return OK;}int main(){    SqStack S;        if (InitStack(&S))    {        SElemType e;                int i;        printf("init_success\n");                if (IsEmpty(S))        {            printf("Stack is empty\n");        }                        for (i = 0; i < 10; i++)        {            Push(&S, i);        }        GetTop(S, &e);        printf("The first element is %d\n", e);        printf("length is %d\n", GetLength(S));        Pop(&S, &e);        printf("Pop element is %d\n", e);        TraverseStack(S, *visit);                if (DestroyStack(&S))        {            printf("\ndestroy_success\n");        }    }}